Running strides Part 1: ground and aerial contact times

I'm going to break apart my discussion of running into two posts. This first post lays out the foundations of how to calculate certain elementary running metrics including time spend in the air per running stride and time spent on the ground. Consider this an expansion of my previous discussion on the short life of a foot strike. The second part will use the foundations here to predict some perhaps more original calculations for running, including stride angles and ground forces experienced by a runner. I am not claiming I've discovered any novel numbers per se, but maybe a new approach to obtaining them. That is to come later, however. For now let's consider some basic calculations, for even these results may surprise the curious (scientist) runner.

Turnover rates, R

Let's begin with running turnover rates, which are complex entities but with lots of empirical data to back them up. They are easy to measure but hard to predict. Empirically you just measure a runner's speed and count their strides per unit time. Theoretical turnover rates, which require knowledge of a runner's muscle system, surface stiffness, etc, are by contrast very difficult-to-predict entities.

Stride rate is defined here by R in steps per second. Running at 180 steps per minute translates to 3 steps per second. Alex Hutchinson has already disused in some detail  the degree to which step rates increase with speed. Here is the a plot of his combining several running studies (and some self-reported numbers) on turnover rate. Note his plot show steps per second of a single leg, not both, hence the numbers are half of the total turnover (180 strides per minute is equivalent to 1.5 strides per second per leg). Here is Alex's combined data set for turnovers for various runners:

Figure 1: Turnover rates at variable speeds

Specifically what has been discussed already is that the stride rate is not constant. Despite Jack Daniels' claim that R ~ 180 steps per minute, empirical evidence shows that turnover rates increases  monotonically from walking speeds up to Olympic-grade sprinters.  That much is clear from looking at figure 1. As you increase you speed, so does your turnover rate.

But what I'm interested in finding out is whether you can describe this relation semi-empirically or not. For instance, not only does one's turnover rate increase with time, but it appears to do so quadratically. In other words the turnover rate R looks like this:

Here v_x is one's forward velocity in meters per second [m/s]. Typical running speeds range between 2.5 and 7 m/s (9 and 25 km/h) for distance runners, and can reach as high as 12.2 m/s for sprinters. Furthermore, it seems that turnover rate obeys the physics of a swinging pendulum, where the the period of swing T (in seconds) is

where l is the length of the object and g is the force of gravity. R has units inverse seconds so that R = 1/T. Applying this idea to running, we expect that runner with longer legs to have a slower turnover rate. We can modify the above equation accordingly like so:

Here L is the length of our hypothetical runner's leg. A runner with legs 10% longer (say 0.91 m vs 0.99) should have a slightly slower turnover, in this case of about 5%. Alex Hutchinson talked about a leg's pendulum action with respect to turnover rate in a Sweat Science post. He found this law is reasonably obeyed with real running data.

Our equation is semi-empirical since we've applied fundamental physics for the effects of leg lengths but the the quadratic relation with v_x is based on observation alone. Assuming a single constant height for an athlete, we can ignore the square root in the denominator and just use the original equation for R. Here is some empirical data for stride length and rate:

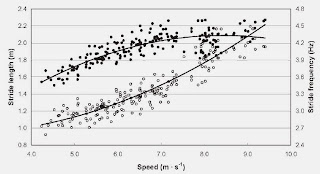Empitical stride rate and stride length. Empirical data from Nummela et al. 

More empirical data for stride length and rate

Turnover rates vary by athlete, but I made a simplified formula that approximates the empirical data. In Hz (1/s),

I found I could use a quadratic value for R with respect to speed and ignore the linear term. To determine the stride length divide the forward velocity v_x by R.

D_tot is then the total distance covered per stride (in units of meters per step). We can rewrite the above equation as

Here is my own data

Considering the small amount of input information this graph is a reasonably good start to what I want to talk about next.

Ground contact and aerial running phases

I'm now going to divide the up the time spent by each footstep into two parts. Take a look at figure 2, which divides the time spent while running on the ground (ground contact time; GCT) and time spent in the air (air time; AT) using one's centre of mass (COM) as a reference. You COM is defined as zero when standing, negative while in the stance/contact phase (think of the knee being bent) and positive when in the air, i..e when both runner's feet temporarily leave the ground.

Figure 2: takeoff angles as a function of speed

Here is a crude diagram showing a runner in the push off phase, and with their front leg about to make contact with the ground.

Theoretical model of ground contact times for a 1.8m tall runner. Although GCT decreases monotonously with speed, the aerial time (AT) is predicted to at first rise from zero (i.e. walking), then drop with faster speeds.

The distance covered during the ground contact time (D_step) is roughly equivalent to the length of your leg, L_leg. Typical leg lengths are about half a person's height. For a 1.8 meter tall person that translates to about 0.9 meters of leg length. The length of your running step remains roughly constant for variable running speeds. It might sound peculiar that I should claim D_step remains unchanged at faster running speeds. First, the reason is that one's leg appears to extend further behind as you move faster is because most of this extension occurs after the push-off (hence the leg kicks farther behind during follow though, like the swing of a bat). If you need convincing this assumption is true, take a look at the range of running motion at various speeds using real people. Then compare our estimated ground contact time (GCT) per step with actual values. Read on.

Below are gait analyses (from this paper), which found that the knee bends in about the same as speeds increase. Mind you, the knee extension is shorter for less experienced runners. But if running "ideal" form, the knee straightens a full 180 degrees behind you and 22 degrees in front. Doing some trigonometry we find one's step length about equal to length

Here is the full cycle of thigh and knee angle for two runner types: one showing an average runner and the second an "ideal" technique by Peter Snell.

The dotted and dashed lines are at different speeds but show little variation in terms of maximum knee angles. In order to calculate the ground contact time (GCT) we divide the step length by the speed.

(again, where the step length remains constant with respect to vx).

The aerial time is then just the time taken per step cycle (1/R) minus the GCT.

Aside: The airborne distance is the difference between total step length and the distance during the contact phase:

The above equation won't be useful yet, so I will save this for part 2. 

Figure 3: GCT and AT phases in running

Let's see what figure 3 means in terms of our understanding of a runner. We have two phases in figure 2, and figure 3 shows the prediction we made of how long is spent in each one at variable speed. What's really interesting is that the aerial time at first goes up (as we expect), but then goes down above ~ 7m/s. The decrease is due to an ever-increasing turnover rate. If focusing on the span of running speeds between 4 and 9 m/s, the aerial time appears to stay nearly constant around 150 ms, which broadly agrees with the literature. Meanwhile the GCT goes down with ever faster speeds. Are these numbers reasonable? Below is the empirical counterpart to these same measurements:

Figure 4: Ground contact time is filled circles; aerial time is empty. Empirical data from Nummela et al. Note the shape of each curve set is similar to the theoretical model. GCT decreases linearly with speed, though other studies find the decrease is second-order. The AT phase is more complex, and in this study ends a 4 m/s. A full span at slower speeds could be revealing. 

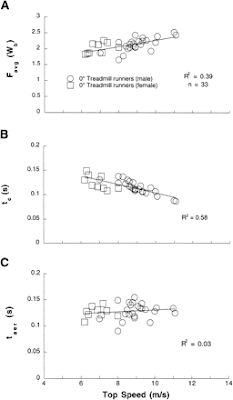Figure 5: from this paper. Tc is ground contact time and Taer is aerial time. I included ground contact force, as it will be used in an upcoming post.

Comparing time of my model for, say, 5 m/s, the model predict GCT = 200ms and AT = 142 ms.
figure 4 estimates GCT = 180 ~ 210 ms and AT = 130 ~ 170ms. Extrapolating, Figure 5 measures runners at 5m/s around GCT = 150 ms and AT = 110 ms. Figure 5 C data shows much lower contact times, i.e. 230 strides per minute at a "low" running speeds of 5-8 m/s. This is because their study was for novice runner's top speed, so that in order for them to reach these speeds, they have a much higher turnover at a given speed than a seasoned athlete.  Overall, GCT is mostly dependent on how fast you are turning your legs and how fast you are actually moving forward.

I use these two example to show that empirical data itself has wide ranges of data, so it's not a serious concern if numbers mismatch a little. (also there are inherent differences between results obtained on treadmills vs over ground). The above two papers estimate contact times and ground our calculated results. For instance, if our assumption about a constant leg contact distance were incorrect we'd see real contact times noticeably longer at faster speeds than my predicted ones. The stance phase is shorter than expected (figure 5), but the results largely agree with figure 4. Moreover, stance phase times differ depending on softness of surface, steepness, individual variability between runners and equipment used to do measurements. All of this is to say my values agree in shape and within standard error of independently-measured data sets.

Summary

So it looks like both the aerial and ground contact predictions are reasonable, hence our underlying assumptions for the equations of R and D_step are reasonable. The equations I've used are pretty simple, so it's not surprising that the calculated values agree with empirical ones. I have't been able to predict why the turnover rate increases the way it does, but from now on I will use these values to create semi-empirical predictions and comparing them with other data which is normally found using empirical-only measurements.

For the second part I'm going to expand on these contact/aerial phase equations and calculate reaction forces, impulses times and  takeoff angle of a hypothetical "ideal"  runner. And while calculating these values I will also predict the speed at which one transitions from a walk to a run (without employing the Froude number, which is the standard method of estimating this transition point). Until next then, happy runnings.