The two-hour marathon: Can it happen? The debate heated up with Dennis Kimetto's time of 2:02:57 in the fall of 2014. As I recall, he was less than a kilometer from the finish when he crossed the two-hour mark. But even before Kimetto's run, Alex Hutchinson had already assembled a discussion on what it would take to run a sub 2-hour marathon.
I have been watching these debates mainly from the sidelines as I hadn't found the data convincing enough either way. The only truly convincing (though most difficult) demonstration would be to run a 1:59:59 marathon. The easiest -and most problematic- line of reasoning is to plot marathon record time vs date achieved and extrapolate to one's peril:
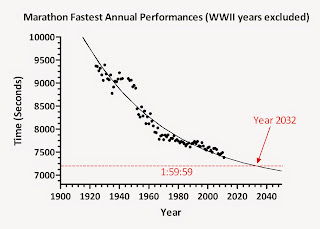 |
| Image from SweatScience's post 2032: Year of the Sub-2:00 Marathon? |
Many of the arguments for (and against) a 1:59 marathon seems to hinge around quite specific 'hows' and 'whens'. In particular, there is much prediction of details such as day-of air temperature, the year we might see it happen (see above plot), on which course it will happen, the wind speed/direction, runner's age, runner's height/weight, and time of day. Whether separate or combined these numbers make for poor model predictors. I know of no strongly predictive function that readily incorporates these variables
Marathon time = (Temp,wind,hills,VO2max,height, height, ???)
As much as details can matter in retrospect, they are not easy tools to estimate future performance (consider Wanjiru's 2008 Olympic gold, for one). After reading many an article, the sub-2-hour mark seemed like one of those things that might be possible, but who really knows.
Taking another look
Although I have nothing at stake, I found two additional lines of reasoning that seem to argue (to my surprise) in favour of a sub 2-hour performance: one argument is mostly empirical, the other mostly experimental (empirical). Conveniently, the background material for both approaches appears in the same blog post.
The mostly-theoretical Argument:
Peter Reigel's formula, though popular and somewhat useful, is not always a suitable predictor of precise performances including those of professionals. As a refresher, here is the often-used formula:
T is time and D is distance. Knowing your time for one distance allows you to predict time for another. I know the Riegel formula has been invoked to argue against a two-hour marathon, as it would imply such a runner would complete the half marathon in 57:30, almost a minute faster than the current world record (58:23)
T = 119.9min*(21.1/42.2)1.06
= 57.5 min
Since Reigel's predictor only works in ratios, I used the more relaxed condition that includes a second term, k, that permits absolute predictions (given at least two race distances to work with):
This relation is known as the Power Law, and there are a few papers that use this more flexible arrangement, such as here or here. Of course you can obtain the original Reigel formulation so that k cancels and m = 1.06. But more interesting is to take the log of both sides and obtain linear fits for each runner.
Plotting lnT vs lnD (where slope = m and intercept = ln(k)) yields customized k and m values per athlete. The goal of the curious researcher is to extract these values, k and m, and compare with a collection of runners. The goal of the athlete is to train, hence minimize m (fatigue resistance) and k (endurance-speed).
As an example, let's use a semi-randomly chosen athlete Serhiy Lebid, who recently set a marathon PB of 2:08. Using this value and other IAAF-approved personal best times, I plotted the log(time) vs log(distance) to obtain his m and k's (where k = exp(-2.44)):
 |
| Tabulated values for linear plot |
 |
| Serhiy Lebid's log-log plot |
From Lebid's PB times -ranging from 1500m to the marathon- the fit is quite good, with R-squared = 0.9998 and (m,k) = (1.071,0.0869). Notice m = 1.07 and not 1.06, as in the default Regiel ratio. Generally I find the R-squared correlations in the power law to be > 0.999 for almost any runner, which is rather impressive for such a simple equation. My favourite fit is for Eliud Kipchoge, whose Reigel fit is an almost perfect 0.999998 using six events spanning the 1500m (3:33) to the marathon (2:04:05).
Returning to the question of the 2h marathon, if we assume the power-law formula is an accurate representation of a given athlete, we can solve the equation for T = 2h (7200 s) and D = 42200m. Then we have one degree of freedom; a line in which k is a function of m:
In choosing a few semi-realisitc values of m (1.01 to 1.11) we can draw a line in the sand, so to speak; one side for those who run sub 2-hour marathons, and everyone else (so far literally everyone):
 |
| Moving south of the line guarantees a place in world history |
 |
| Purple dot: My predicted crossing point for the first sub-2 hour time |
As you might have guessed, none of the points (yet) lie below the sub 2-hour curve. But many athletes lie extremely close, and, interestingly, at different locations on the line. The red circle on the very far right belongs to Dennis Kimetto (current marathon WR holder), whose m = 1.01 seems suspiciously low, likely because his PBs only include the 10k, half and full. Were he to run middle distance races, the x-y position would likely change (but maybe not?). The majority of runners cluster around m values of 1.05 to 1.07, and k values of 0.08 to 0.12. Nevertheless, the spread is significant, which implies, as one might intuit, there are several ways to be competitive at a given distance.
Aside: For perspective, here are the optimal curves for three distances (1500m, 10k, and marathon) for as-yet unbeaten times. They are similar, but not identical; the contour lines that define an excellent marathoner may or may overlap with a skilled middle distance runner.
Realistically, what might a sub 2-hour runner look like at distances other than the marathon? There are an infinity of solutions, but some appear more likely than others. In choosing m values > 1.05 I found unrealistic times for shorter distances (for instance 7:16 for 3k). I found the most realistic predictors across all distances were when k = 0.111 and m = 1.04.
These values predict our sub-2 hour marathoner could run (realistic) shorter distance times such as 7:40 for 3k and 26:48 for 10k. Though barely a 4-minute miler, he would excel dramatically as distances increase. Hence the most likely candidate for the sub-2 hour mark has an extremely high resistance to fatigue; his speed will only decrease by a few percent when racing longer distances. All predicted times are not faster than record times except the half marathon (but only by 6 seconds, instead of the earlier 53 seconds) and -of course- the full.
Where might this amazing hypothetical person come from? One might suppose were someone capable of a sub-2 marathon he would have to rapidly graduate from track to the road, as working on speed will not help nearly as much as fatigue resistance. Perhaps they will skip shorter distances entirely. Or we might need to have the marathon run on a track. All in all, the implications are, somewhat to my surprise, that such a person may actually exist.
The mostly-empirical Argument:
I have mentioned in my previous blog that women slow with respect to men at longer distances (but no worries; women improve compared to men in swimming events!). In shorter running events, elite women are about 8 to 10% slower than men. For longer distances, the relative difference is about 12-14%. But what really caught my attention was that for some reason there is a dip at the marathon distance. I know what many are thinking: the dip is because of Paula Radcliffe's amazing 2:15 performance. Not so! I chose the 5th fastest person-time for all distances, male and female, for this very reason. Taking 5-fastest person ratios eliminates single person outliers (e.g. Bolt, Flo Jo, and the chinese 3k contingency who've been suspected of team doping but never caught). Hence the marathon-specific ratio is obtained via the non-Radcliffe/non-Kimetto times 2:18:59/2:03:58 = 1.121.
 |
| Elite male and female runners' ratios. Time ratios are of the 5th fastest person (not time) ever run for a given distance. Top lists are from IAAF |
How does this observation lead to a sub two-hour marathon? Assuming women *should* be racing 13% slower for the marathon than men, and not 12% (currently the case), then taking a ratio of Paula Radcliffe's marathon time with a hypothetical male counterpart....
2:15:25/X = 1.13
[drum roll]
X = 1:59:50
Were there a male out there who could run 13% faster than Paula, that would automatically imply a sub-2 hour runner should exist. Since top men at other distances are already 13% faster than females at the same distance this example is not as cherry-picked as it might first seem.
Summary
I have provided two arguments, one based on empirical reasoning, the other theoretical. These arguments have shown, to my own initial surprise, that a sub two hour marathon may in fact be possible. Nevertheless, by definition I am extrapolating from the present. These are only predictions, not proofs. By tweaking the numbers even slightly, one could just as easily cast doubt on my claims (maybe Radcliffe's time is not a good reference point? Maybe the power law is not suitable for predicting marathon distances?).
As runners edge closer to the 120 minute mark, one should remain open-minded to exciting new possibilities in sport performance. I am skeptical by nature, and encourage likewise in others. What I claim to hold true in my discussion above is that if a two-hour runner were to emerge, although he would be an incredible athlete, he would not be superhuman. By comparing his performance at other distances (via the power law), and relating his time to the best female marathon runners (via the F/M ratios), a 1:59:59 performance would not appear as an extreme outlier in either case. Rather, he would remain within the anticipated limits of human (male) performance.
Until such a runner emerges, there is nothing to do but wait, train, and debate. Hopefully we are not waiting for Godot.
 |
| "When will that 2-hour marathoner show up?" |


